CLUSTER REPLICATION AND LOGARITHMIC SCALABILITY

If you have been using cluster replication with some open source operational database, you might have noticed that they do not scale out well. If you are interested in knowing why, this is the post to read. Cluster replication was introduced in the mid-1990s as a way to scale out databases.
The basic idea, which is called full replication (most commonly known as cluster replication), is to have a cluster of server nodes, each of them running a database engine with a full copy of the database. But how do we keep all replicas consistent and up to date?
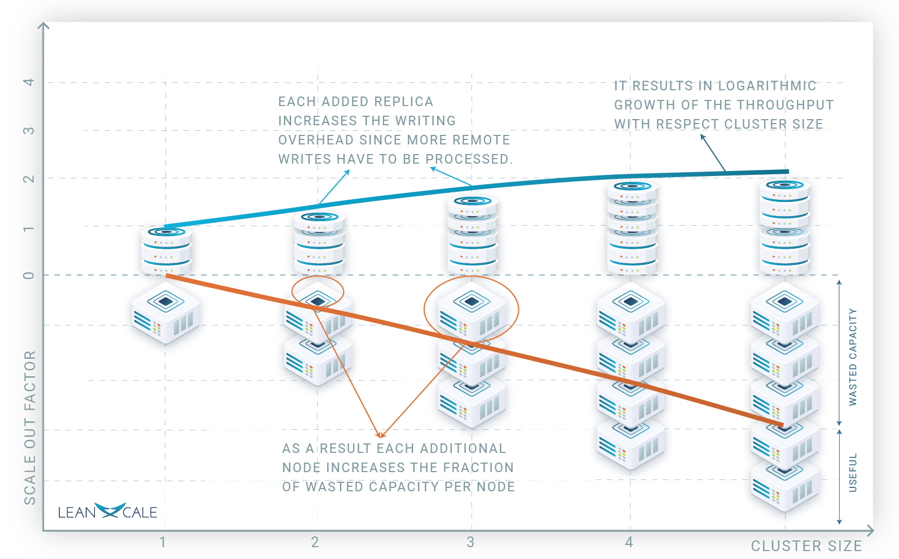
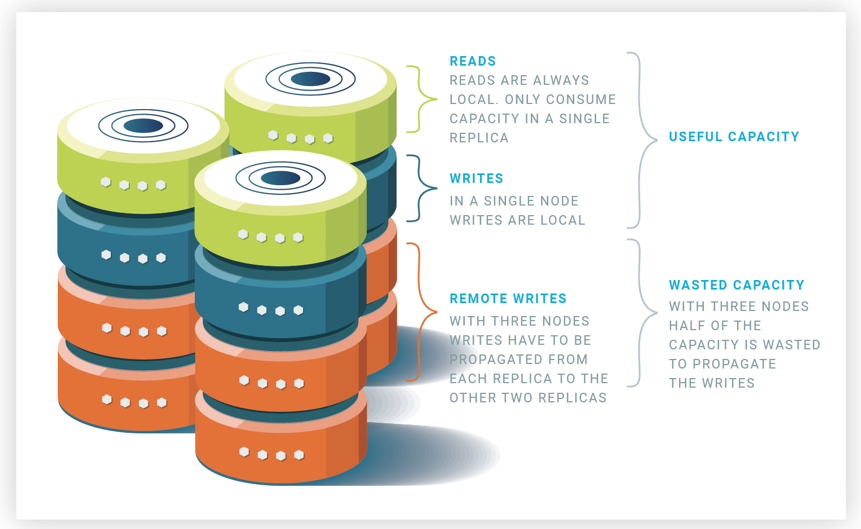
The strategy typically used to update the replicas is ROWAA (Read One Write All Available), where each read operation is executed on any one replica while a write operation is executed on all replicas. So, what is the scalability of cluster replication? On one extreme of the scalability spectrum, if we only have writes in the workload, we have null scalability, since all replicas do the same and the cluster throughput is the same as that of a single node, i.e., it does not scale. On the other extreme, if we only have reads, assuming a uniform load across replicas, we have linear scalability, i.e., a cluster with n replicas has a global throughput equal to n times the one of a single node. In between, we have logarithmic scalability, that is, the cluster throughput only grows logarithmically when increasing the number of nodes. The reason is because the bigger the cluster size, the higher the wasted capacity per node. Figure 1 depicts graphically what happens.
On the lower part, we see how many servers we have for a particular cluster size. The orange line indicates how much capacity of the servers is wasted, i.e., the space between the x axis to the orange line is the wasted capacity.
SCALABILITY FACTOR
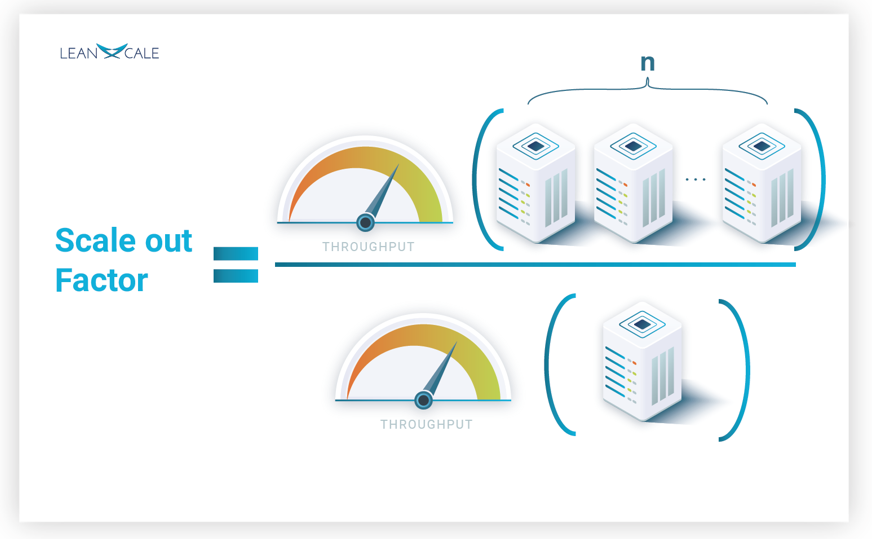
But how can we actually quantify scalability? We devote the rest of the post to it. Let’s develop our analytical model. Firstly we do it intuitively, and then we formalize it mathematically. A database with cluster replication is able to process a number of read and write operations, that is, it is able to deliver a certain maximum throughput. We can make the throughput relative to that of a single node, this is what is actually called the scale out factor [Jiménez-Peris et al. 2003]. To get the scale out factor, f, we simply divide the useful work, which is the actual throughput, by the total amount of work (see Figure 2). The optimal scale out factor is the size of the cluster. That is, for a cluster of n nodes, the optimal scale out is n.
EFFICIENCY OF 1-NODE CLUSTER
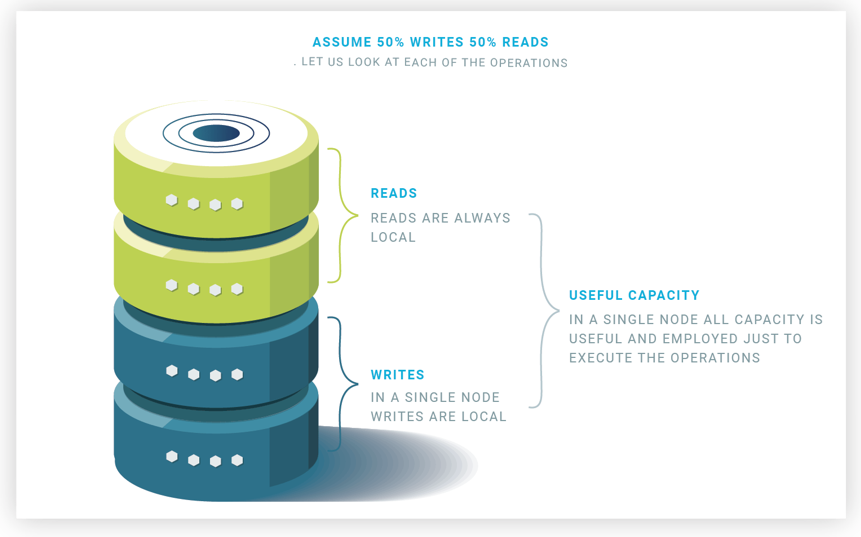
Let’s consider a workload with 50% reads and 50% writes. For simplicity, assume the cost of reads and writes are the same. The single node will devote half of the capacity to execute writes and the other half to execute reads. If we execute a read and a write, the throughput will be 2 operations (the read and the write) and the work done 2 operations (the read and the write) as well, so f=2/2=1. This is easy (see Figure 1).
EFFICIENCY OF 2-NODE CLUSTER
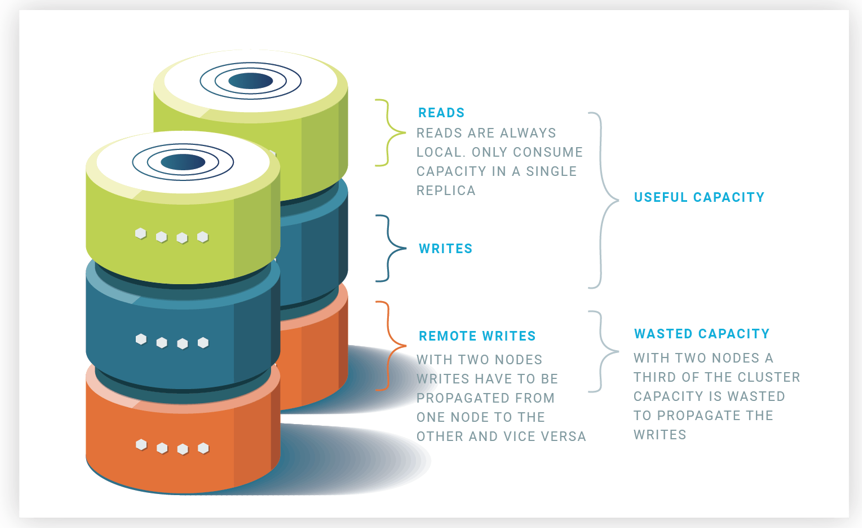
Let’s now look at a cluster of two nodes. Each node wants to execute one read and one write. However, each write executed at the other node also must be executed locally. We call it remote write. Thus, each node will do its local read, its local write, plus a remote write, meaning that 2/3 of the capacity of the nodes is employed for useful work. Note that this means we are wasting 1/3 of the capacity of each node doing remote writes. This is the price of full replication, executing writes everywhere. So each node of the two nodes does three operations: one read and one write plus the remote write, thus: f=2•(2/(1+1+1)=4/3=1.33. In other words, the two nodes deliver the same throughput as one node and one third of a node.
EFFICIENCY OF 3-NODE CLUSTER
Let’s take a look at a three-node cluster and from there we can easily generalize the formula for an arbitrary cluster size. If we have 3 replicas, each replica processes 1 read and 1 write, but will also have to execute two remote writes corresponding to the writes from the other two replicas. Therefore, they execute four operations (the read, the write and two remote writes), but only two are useful work: f=3•(2/(2+1+1))=6/4=1.5.Having 3 replicas we attain throughput 1.5 times that of a single node, that is, half of the 3 node cluster capacity is wasted.
SCALABILITY ANALYTICAL MODEL
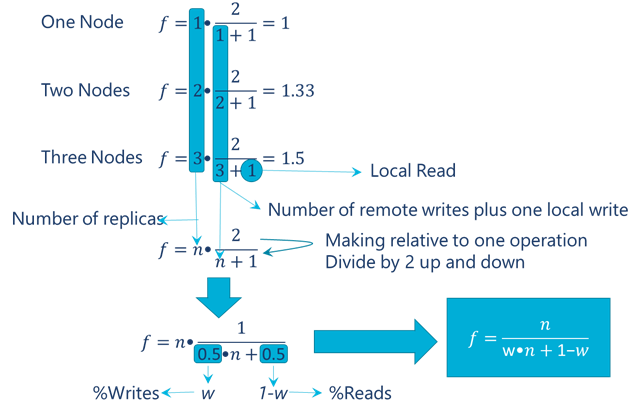
In the box below, we generalize for a cluster with n replicas and generate the mathematical analytical model. If you are not interested in the math (Figure 6 shows the inference of the model in a visual intuitive way), just skip the below box.
With a one node cluster the ratio between useful work or actual throughput and total work done of the system is 2 operations (1 read & 1 write) and the work done is actually 2 operations, so we have that the scale out factor is the amount of useful work (the two operations) divided by the total amount of work as depicted in line “One Node” in Figure 6. With two nodes for performing the two operations, but the work actually done is two writes and one read as shown in line “Two Nodes” in Figure 6. And with three nodes we still do two operations of useful work but a total work of three writes and one read as seen in line “Three Nodes” in Figure 6. The generalization for n nodes is easy and it can be seen in Figure 6. We can make the figures relative to one operation (we were considering two operations, one read and one write) as shown in Figure 6. The first 0.5 corresponds to the fraction of writes (50%) and the second to fraction of reads (also 50%). To make it general for an arbitrary fraction of reads and writes, if the fraction of writes is w, then the fraction of reads is (1-w). The final formula is shown in the blue box in Figure 6.
EXAMPLE: SCALABILITY WITH 50% WRITES AND 50 % READS (W=0.5)
With our analytical model, we can now obtain f for any value of n and w. For w=0.5 (50% writes) and nvarying between 1 and 10 we get the table on the left of Figure 7.
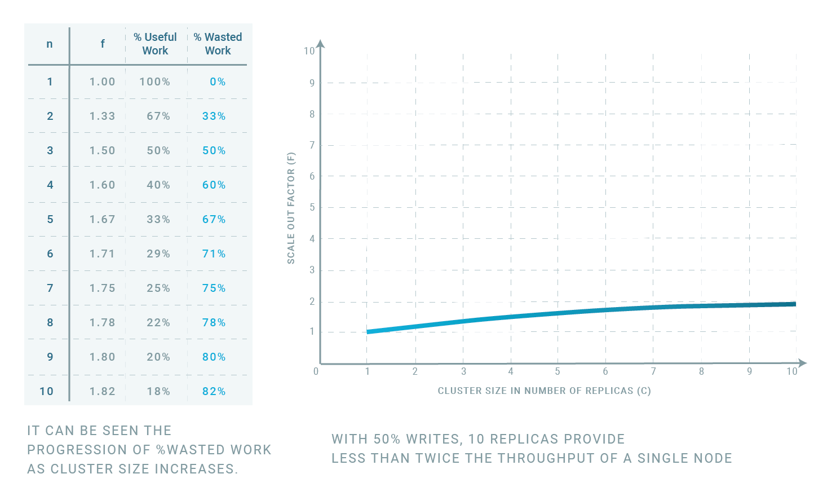
As we can see for 10 nodes, each node is contributing very little useful work, only 18%. Thus, 82% of the capacity is wasted in applying the writes from the other 9 replica nodes. Note that the ideal should be f = n, i.e. %Useful Work = 100% and %Wasted Work= 0%. In the graph of Figure 7 we can see the shape of the scalability, a logarithmic curve.
SCALABILITY OF ALL WORKLOADS (0<= W <= 1)
Let’s take a global look for all workloads (values of w between 0 and 1) and cluster sizes from 1 to 10. The result is shown in the graph of Figure 8.
As we can see, with 50% writes, it is not really worth doing cluster replication to scale out. To get 50% that a single node can do, we will need 3 nodes. And from there, any additional node will provide a neglectable additional capacity. With 20% writes, cluster replication can help to improve the throughput, yet at a high cost. A cluster with 10 nodes will deliver only 3.57 times the throughput of a single node, so 64.3% of the capacity is wasted for the overhead of replication.
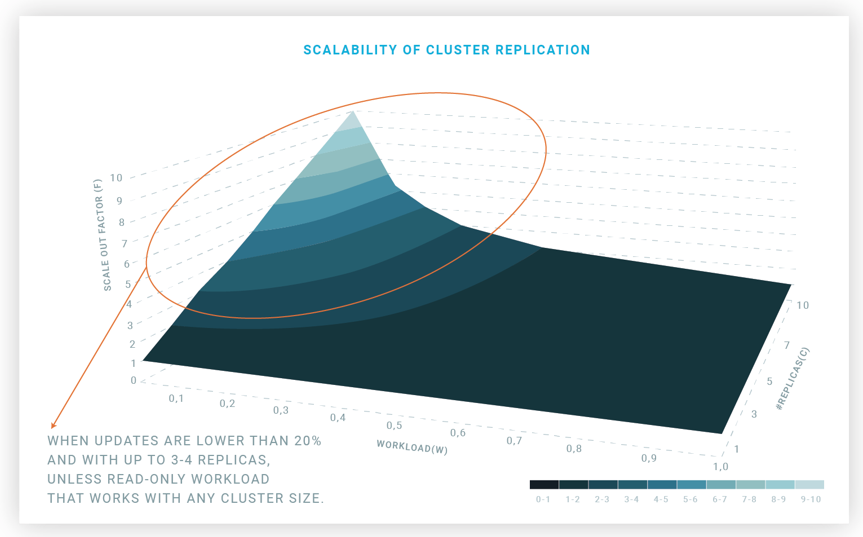
To summarize the discussion, if there are only reads, scalability is linear so the scale out factor is the same as the cluster size. If there are only writes, scalability is null since, for any cluster size, the scale out factor is always one. This means that the delivered cluster throughput is that of a single node, so it does not matter how many replicas we add.
If you become more interested in how to analytically model the scalability of cluster replication solutions, you can read the paper [Jiménez-Peris et al. 2003] where, with some colleagues in the early 2000s, one of us created an analytical model to compute the scalability of cluster replication.
OVERHEAD OF REPLICA CONSISTENCY
The overhead of updating replicas is not the only issue. Another major issue is how to maintain replica consistency, which implies executing conflictive update transactions in the same order for all replicas. This replica consistency is hard to achieve without damaging performance. There are different ways of doing replication. Cluster replication generally uses a master-lazy approach (see our blog post on database replication techniques). The master-lazy approach works as follows (see Figure 9). One replica out of all the replicas in the cluster is distinguished as master. The master (also called primary) is the one executing all update transactions.
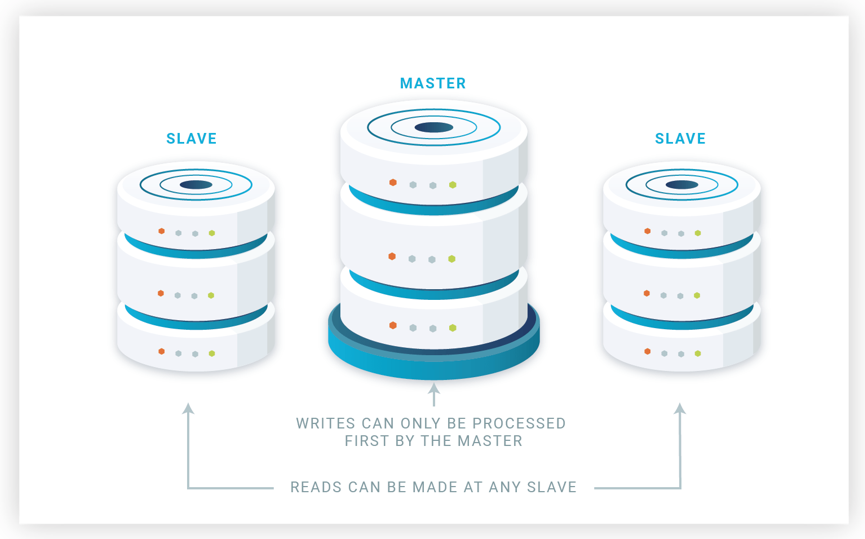
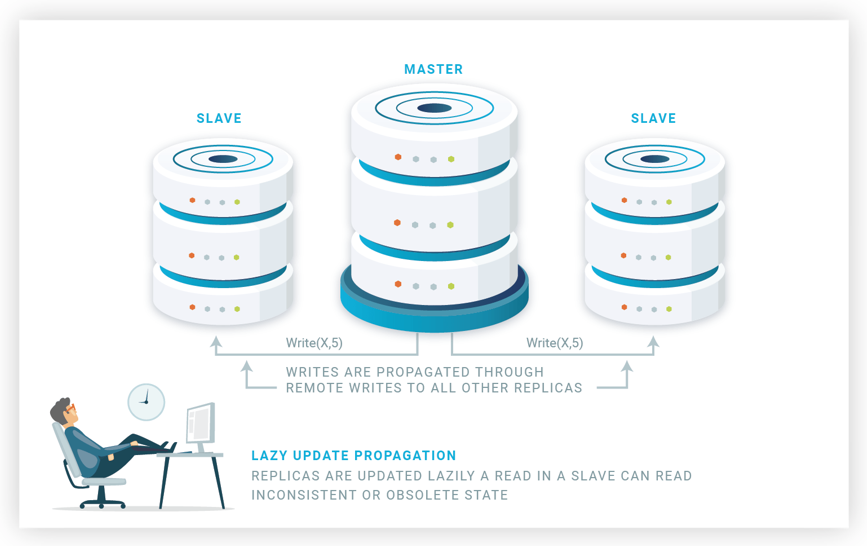
The master lazily propagates the updates of committed transactions to slave replicas, also called backups (see Figure 10). That is, update transactions are propagated asynchronously, which results in not guaranteeing replica consistency, just eventual consistency. Replicas commit the update transactions in the same order they were committed to the master.
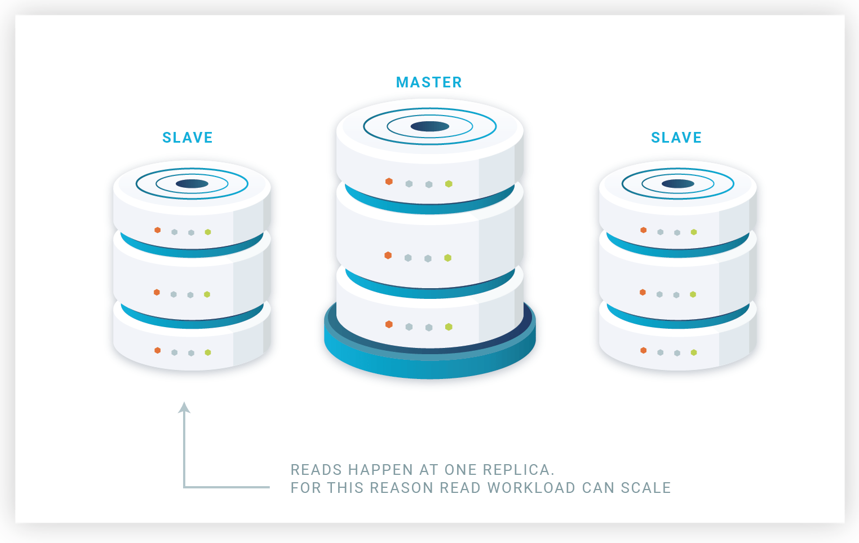
Read only transactions are executed at the slave replicas (see Figure 11). Slave replicas are not up to date due to the lazy propagation of updates but provide an older version of the database. One can wonder whether update transactions could be committed in parallel for the slave replicas. It can certainly be done, but then the replica consistency provided is null. By committing in the same order as the master, the slaves generate the same serialization order of the database. So read-only transactions observe older snapshots of the data than they should, however they at least observe snapshots that existed at the master.
IS EAGER REPLICATION AN ALTERNATIVE?
But is it not possible to provide full replica consistency in cluster replication? Yes, it can be done by means of eager transaction propagation. But eager transaction propagation requires to the commitment for all replicas to be coordinated through a distributed agreement protocol. The way to coordinate the commitment across all replicas is to use the popular two-phase commit (2PC) protocol, which guarantees that all transactions are committed atomically across all replicas. 2PC is heavyweight and exhausts the IO bandwidth because all replicas have to commit all transactions synchronously. However, this is especially slow because transactions are committed one by one cluster wise. This is why cluster replication typically relies on a lazy approach.
MAIN TAKEAWAYS
Cluster replication scales logarithmically, so it only makes economic sense to use it with a cluster with a few replicas and a low percentage of write operations. The main strategy used by replication protocols for cluster replication is Master-Lazy where all update transactions are executed at the master and updates are lazily propagated to the slaves. Slaves just execute read-only transactions.
REFERENCES

[Jiménez-Peris et al. 2003] Ricardo Jiménez-Peris, Marta Patiño-Martínez, Gustavo Alonso, Bettina Kemme. Are quorums an alternative for data replication? ACM Transactions on Database Systems, 28 (3), 257-294, 2003.

[Jiménez-Peris et al. 2003] Ricardo Jiménez-Peris, Marta Patiño-Martínez, Gustavo Alonso, Bettina Kemme. Are quorums an alternative for data replication? ACM Transactions on Database Systems, 28 (3), 257-294, 2003.
RELATED BLOG POSTS

ABOUT THIS BLOG SERIES
This blog series aims at educating database practitioners in topics commonly not well understood, often due to false or confusing marketing messages. The blog provides the foundations and tools to let the reader actually evaluate database systems, learn their real capabilities and be able to compare the performance of the different alternatives for its targeted workload. The blog is vendor agnostic.
ABOUT THE AUTHORS
- Dr. Ricardo Jimenez-Peris is the CEO and founder of LeanXcale. Before founding LeanXcale, he was for over 25 years a researcher in distributed databases director of the Distributed Systems Lab and university professor teaching distributed systems.
- Dr. Patrick Valduriez is a researcher at INRIA, co-author of the book “Principles of Distributed Databases” that has educated legions of students and engineers in this field and more recently, Scientific Advisor of LeanXcale.
ABOUT LEANXCALE
LeanXcale is a startup making a NewSQL database. Since the blog is vendor agnostic, we do not talk about LeanXcale itself. Readers interested in LeanXcale can visit the LeanXcale website.
Sponsored by LeanXcale